
INTRODUZIONE ALL'IPERSPAZIO
INTRODUCTION TO HYPERSPACE
(La Nativita' vista da un fisico)
INTRODUCTION TO HYPERSPACE
(La Nativita' vista da un fisico)
SECONDO LE VISIONI DI MARIA VALTORTA CI SEMBRA CHE LA NASCITA VERGINALE DI GESU' SIA SPIEGABILE CON LE PROPRIETA' DI UNA QUARTA DIMENSIONE (VEDI LINK A FONDO PAGINA)
L'IMMAGINE CONTENUTA NEL LINK NON E' COPERTA DA COPYRIGHT E PUO' ESSERE RIPRODOTTA E DIVULGATA OVUNQUE
INTRODUZIONE ALL’IPERSPAZIO
(ovvero la Natività, spartiacque della storia, vista da un fisico)
(ovvero la Natività, spartiacque della storia, vista da un fisico)
In appendice: L'Equazione del Bambino (The Kid Equation, 24 giugno 2008)
1. GENERALITA’
Uno spazio si dice ad n dimensioni quando, in un qualunque sistema di riferimento interno a tale spazio, sono necessari e sufficienti n coordinate per definire la posizione di un punto appartenente a quello spazio (n intero ≥ 0).
Ad esempio la retta r della figura 1, rappresenta uno spazio ad una dimensione (o monodimensionale, o di ordine uno) perché fissata un’origine O, un verso ed una unità di misura con cui graduare la retta stessa, con un solo dato (la coordinata del punto, che dipende dall’unità di misura e dal verso) è possibile individuare la posizione di un punto P che appartiene a tale spazio.
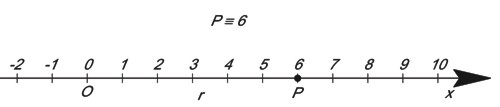
Figura 1 - Uno spazio monodimensionale
Con un generico riferimento cartesiano (per generalizzare in figura 2a abbiamo adottato coordinate oblique) su di un piano a curvatura nulla (piano euclideo), i dati necessari sono due, l’ascissa x e l’ordinata y.
Anche nel caso della figura 2b, in cui viene rappresentato un sistema di riferimento a coordinate polari, sono necessari due dati: il raggio vettore ρ (avente origine nel polo O, appartenente alla retta r, e modulo proporzionale all’unità di misura adottata) e l’anomalia φ (0≤φ≤2π) misurata a partire da r ed in senso antiorario.
.jpg)
Figura 2a – Coordinate oblique Figura 2b – Coordinate polari
In base alla definizione data il piano euclideo è uno spazio bidimensionale.
Nel caso della figura 3, abbiamo una rappresentazione prospettica di un sistema di riferimento cartesiano ortogonale, costituito dalle rette orientate x, y, z aventi un’origine comune O: poiché sono necessari tre dati per individuare la posizione di un punto P, sempre in virtù della definizione data, si può affermare che lo spazio ivi rappresentato è tridimensionale (o di ordine tre).1. GENERALITA’
Uno spazio si dice ad n dimensioni quando, in un qualunque sistema di riferimento interno a tale spazio, sono necessari e sufficienti n coordinate per definire la posizione di un punto appartenente a quello spazio (n intero ≥ 0).
Ad esempio la retta r della figura 1, rappresenta uno spazio ad una dimensione (o monodimensionale, o di ordine uno) perché fissata un’origine O, un verso ed una unità di misura con cui graduare la retta stessa, con un solo dato (la coordinata del punto, che dipende dall’unità di misura e dal verso) è possibile individuare la posizione di un punto P che appartiene a tale spazio.

Figura 1 - Uno spazio monodimensionale
Con un generico riferimento cartesiano (per generalizzare in figura 2a abbiamo adottato coordinate oblique) su di un piano a curvatura nulla (piano euclideo), i dati necessari sono due, l’ascissa x e l’ordinata y.
Anche nel caso della figura 2b, in cui viene rappresentato un sistema di riferimento a coordinate polari, sono necessari due dati: il raggio vettore ρ (avente origine nel polo O, appartenente alla retta r, e modulo proporzionale all’unità di misura adottata) e l’anomalia φ (0≤φ≤2π) misurata a partire da r ed in senso antiorario.
.jpg)
Figura 2a – Coordinate oblique Figura 2b – Coordinate polari
In base alla definizione data il piano euclideo è uno spazio bidimensionale.
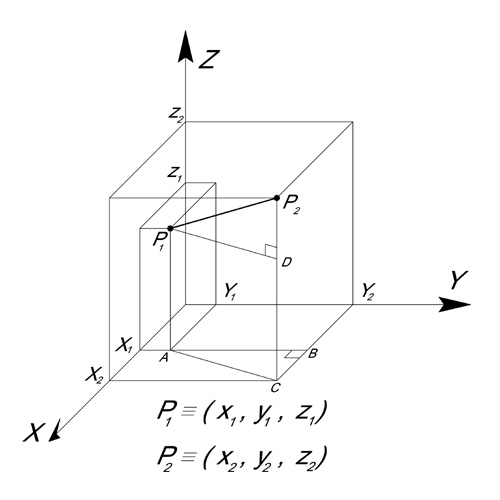
Figura 3 – Prospettiva parallela (assonometria) di uno spazio tridimensionale
Quando n>3 si usa la locuzione superspazio o iperspazio.
Se si volesse rappresentare uno spazio a quattro o più dimensioni ci si troverebbe davanti ad una difficoltà di raffigurazione probabilmente insormontabile; infatti la capacità sensoriale data all’uomo si ferma all’ordine tre, ordine che gode di particolari proprietà, come vedremo in seguito (paragrafo 6).
Qualche matematico ha proposto una rappresentazione prospettica di una sfera di ordine quattro (ipersfera) assumendo, come supporto, una sfera tridimensionale. Certamente la raffigurazione è possibile perché fare la prospettiva di un dato soggetto di ordine n, significa rappresentarlo in uno spazio di ordine n-1, e lo spazio tridimensionale è lo spazio (quello di maggior ordine) da noi percepibile.
Il caso comune (che coinvolge pittori, architetti, disegnatori e cultori di arti figurative in genere) riguarda la rappresentazione prospettica di un soggetto tridimensionale in uno spazio bidimensionale (prospettiva centrale, ovvero con l’osservatore a distanza finita dal quadro). E’ il caso di figura 4: il soggetto, paesaggio tridimensionale, viene rappresentato su di un piano bidimensionale; l’operazione è consistita nel togliere una dimensione al soggetto dato. Il lettore immagini le fatiche dei primi pittori ed architetti che hanno affrontato il problema di carpire alla natura le regole da seguire in tale operazione, che costituiscono quel che noi oggi chiamiamo le regole della prospettiva (Pier della Francesca: De Prospectiva Pingendi del 1485; La Tavola di Urbino, La città ideale; La prima tavola di Berlino; La Tavola di Baltimora; Lo Sposalizio della Vergine di Raffaello etc.).

Figura 4 – Disegnare una prospettiva di un dato soggetto significa rappresentarlo in uno spazio avente una dimensione in meno
Generalizzando, per induzione, ci sembra plausibile affermare che la prospettiva di una prospettiva è priva di significato perché perde contenuti essenziali al riconoscimento del soggetto iniziale.
2. LA DISTANZA TRA DUE PUNTI NELL’IPERSPAZIO
Come è ben noto dalla Geometria Analitica la distanza tra due punti di un piano euclideo
Ed è altrettanto noto che nel caso della distanza tra due punti, in uno spazio tridimensionale e con un riferimento cartesiano ortogonale (come in figura 3), la distanza si ottiene reiterando l’applicazione del medesimo teorema ai triangoli rettangoli indicati in figura, ottenendo:
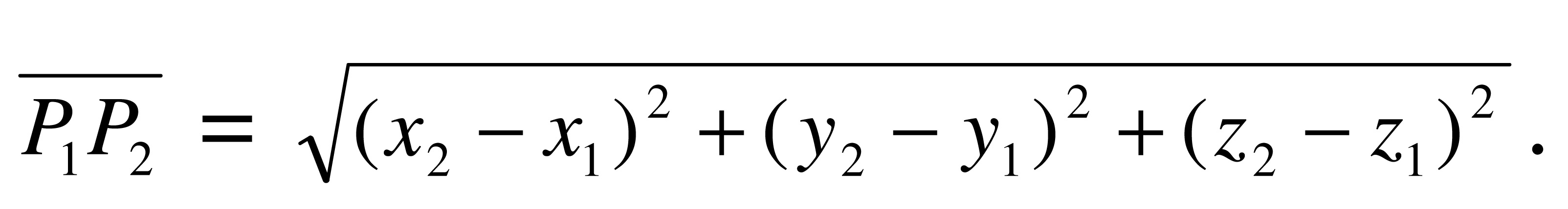
E’ inevitabile convenire che, analogamente, la distanza tra due punti in uno spazio quadrimensionale sia data da:
.jpg)
ove il significato dei simboli è ovvio. Più in generale, la distanza tra due punti in uno superspazio a n dimensioni sarà:
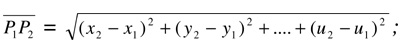
con u n-esima dimensione.
Come appare evidente si possono indagare le proprietà del superspazio con metodi matematici anche se la natura non ci concede l’apprezzamento neanche di una sola quarta dimensione, mutuamente perpendicolare alle tre che ci sono note.
Se riuscissimo ad apprezzare una quarta dimensione acquisteremmo stupefacenti proprietà (alla Gustavo Rol...); e ciò vale per qualunque essere n-dimensionale nei riguardi degli esseri m-dimensionali, quando m<n.
Ci è facile ragionare fino a n=3.
La formichina puntiforme, zero-dimensionale, il cui universo sarebbe costituito da una retta, potrebbe trovarsi in balia di qualunque proprio simile che potesse muoversi in un piano contenente la retta stessa. Infatti questi potrebbe apparire e scomparire senza difficoltà solo grazie alla propria sensibilità della seconda dimensione.
Come sarà fatto l’appartamento di una formichina bidimensionale? Sarà come una piantina topografica dei nostri appartamenti. Ed il moscerino (o la mosca) bidimensionale, ma in grado di percepire una terza dimensione, che proprietà avrà? La figura 5 dovrebbe rendere l’idea: il moscerino, saltando, può entrare in un qualunque punto dell’appartamento della formichina anche a porte chiuse!
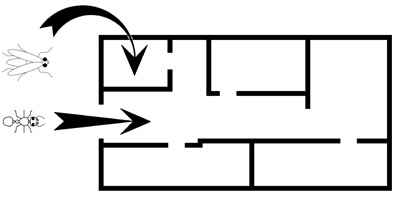
Figura 5 – L’appartamento bidimensionale, la formichina ed il moscerino
Possiamo inferire che noi umani, se avessimo la sensibilità di una quarta dimensione, potremmo entrare ed uscire da casa nostra (ed anche da quelle altrui!) senza bisogno di aprire la porta!
Le proprietà illustrabili sono illimitate; basti pensare alla trasformazione di un guanto bidimensionale da destro a sinistro, e viceversa, come è chiaro dalla figura 6:
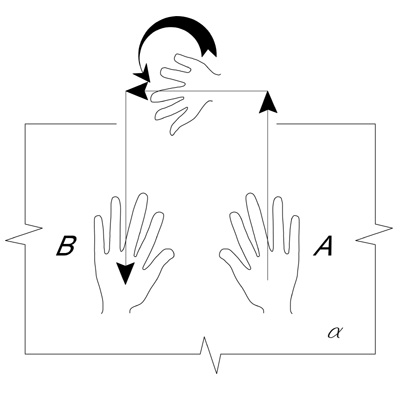
Figura 6 – In A il guanto bidimensionale è destro, una volta rovesciato, grazie all’utilizzo della terza
dimensione, diventa sinistro nella posizione B
3. LA RETTA COME GEODETICA DELLO SPAZIO
La linea geodetica è definita come la linea più breve, giacente su di una data superficie, che congiunge due punti qualunque di quella superficie (comunque curva).
Ad esempio le geodetiche della superficie sferica (spazio bidimensionale) sono archi di cerchi massimi; quelle del piano euclideo sono segmenti di retta etc.
La ricerca delle geodetiche può riservare delle sorprese: prendiamo ad esempio un universo bidimensionale a forma di parallelepipedo come in figura 7:
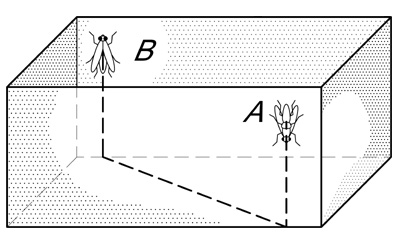
Figura 7 – Universo bidimensionale a forma di scatola
Quale sarà la geodetica che congiunge i due punti A e B? A prima vista verrebbe da dire che la linea ivi tratteggiata sia la più breve. Invece se sviluppiamo la scatola, come in figura 8, scopriamo che la più breve è la linea a tratto misto 1 mentre la tratteggiata di prima è la linea 2 evidentemente più lunga!
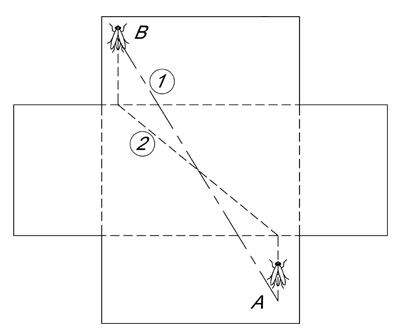
Figura 8 – Per definire la geodetica tra A e B
4. LA CURVATURA DELLO SPAZIO
Il primo principio della Dinamica afferma che un corpo mantiene uno stato di quiete o di moto rettilineo uniforme se non interviene qualche causa esterna (forza) a modificare tale stato.
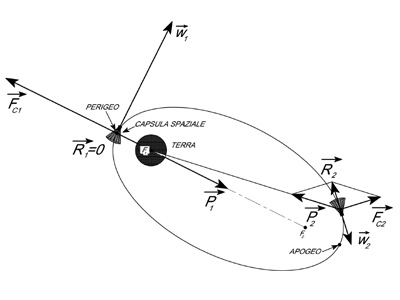
Figura 9 – La navicella in moto inerziale si muove su di una traiettoria geodetica;
con w abbiamo indicato le velocità e con R le risultanti delle forze applicate
(attrazione gravitazionale, o peso, e forza centrifuga).
Per il principio di equivalenza il moto non uniforme della navicella
equivale ad un campo gravitazionale che equilibra ad ogni istante quello terrestre
(ciò implica la coincidenza della massa inerziale con quella gravitazionale)
Questo principio, mutate mutandis, può essere utilizzato per dare una generica definizione di retta (che in geometria euclidea è un concetto primitivo): la retta è la traiettoria seguita da un corpo in moto quando non interviene alcuna causa esterna a modificare tale stato. Quando il corpo segue tale traiettoria “rettilinea” il sistema di riferimento ad esso solidale si chiama riferimento inerziale perché, al suo interno, vale il principio d’inerzia e non esiste esperimento che possa indicare ad un osservatore, ad esso solidale, il proprio stato di moto.
Osserviamo il moto di una navicella spaziale in orbita intorno alla terra, come descritto dalla figura 9: la navicella spaziale costituisce un esempio di sistema inerziale, il suo moto non richiede energia per essere mantenuto. Un osservatore al suo interno non si accorge di muoversi in moto non uniforme (tale è il moto per un osservatore terrestre o solidale ad un altro riferimento diverso da quello della navicella).
E’ come dire che all’interno della navicella effettuando qualunque esperimento sulle masse si riscontrerà sempre la validità del principio F=m∙a.
Se al concetto di retta sostituiamo quello di geodetica possiamo “lavorare” su qualunque spazio, in particolare bidimensionale: ad esempio nella geometria sferica il piano è curvo, come mostrato in figura 10, e la geodetica è un arco di circonferenza massima (meridiano). In tale spazio non vale il celebre V° postulato di Euclide e la somma degli angoli interni di un triangolo è maggiore di 180° (per il cosiddetto eccesso sferico).
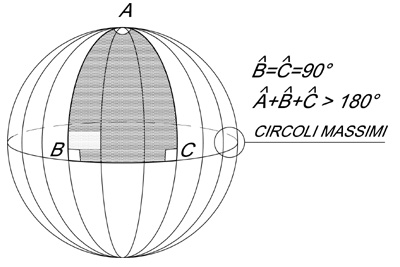
Figura 10 – Nella Geometria Sferica le rette (geodetiche) sono i circoli massimi
e la somma degli angoli interni di un triangolo è maggiore di 180°
5. IL CAMPO GRAVITAZIONALE
Si dice Campo Gravitazionale una regione dello spazio in cui una massa è soggetta all’azione di una forza.
Per la rappresentazione grafica di un campo gravitazionale ci si avvale del metodo di Faraday: nel caso bidimensionale, come nella figura 11, i cerchi concentrici rappresentano le linee equipotenziali mentre le linee radiali rappresentano le linee di forza.
Sia la massa m' quella che genera il campo ed assumiamo la massa m" come massa in osservazione. Ricordiamo che il potenziale di un punto del campo è il lavoro che le forze del campo compiono per spostare la massa di prova (1 kg) da quel punto all’esterno del campo (nel caso in figura a distanza infinita, ove il potenziale sarà massimo ed uguale a zero).
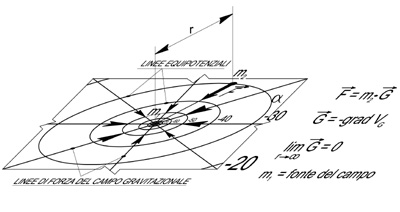
Figura 11 – Nella rappresentazione di Faraday dove le linee equipotenziali sono più “fitte”
le forze sono più intense
Se G è l’intensità del campo e Vgil valore del potenziale in un dato punto, le relazioni riportate in figura costituiscono le equazioni del campo.
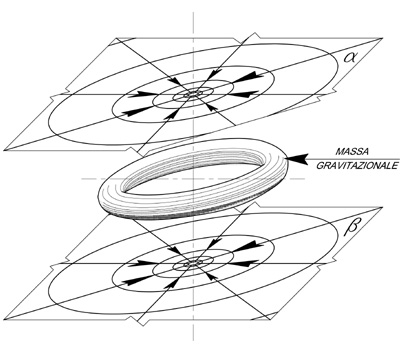
Figura 12 – I due universi paralleli α e β sono incomunicanti tra di loro.
Una massa di forma e densità opportuna, interposta come in figura, può provocare
una deformazione dello spazio (tramite la terza dimensione)
tale da renderli comunicanti
Consideriamo ora due universi bidimensionale e paralleli (immaginiamo due piani euclidei paralleli e sovrapposti come i piani α e β di figura 12 senza l’interposta massa toroidale): gli abitanti di ciascun universo non avranno mai la possibilità di incontrarsi.
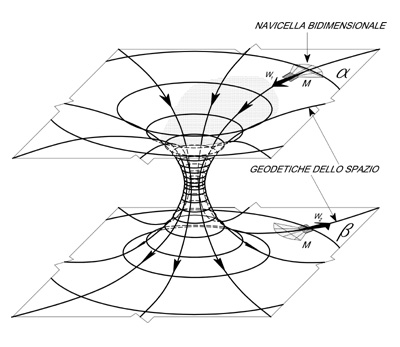
Figura 13 – Curvatura dello spazio in grado di rendere comunicanti due universi paralleli
Però se lo spazio si deformasse, curvandosi, grazie all’interposizione, come in figura 12, di una massa gravitazionale di densità e forma adeguate otterremmo la configurazione illustrata nella figura 13 in cui un veicolo spaziale bidimensionale, in viaggio inerziale, passerebbe dall’universo α a quello β senza nemmeno accorgersi, viaggiando di moto rettilineo uniforme su quella particolare linea retta costituita dalla relativa geodetica.
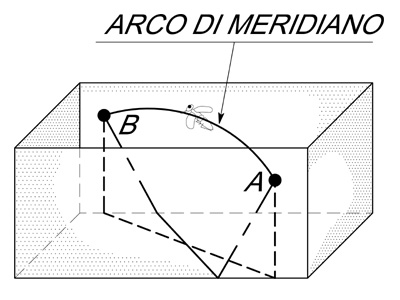
Figura 14 – L’arco di meridiano è la geodetica della sfera terrestre
Ritornando alla nostra “vecchia” mosca: se essa da bidimensionale diventasse all’improvviso tridimensionale (anche se il suo volo non è inerziale, ma per minimizzare l’energia da spendere) seguirebbe una traiettoria geodetica (come un aeroplano) costituita dall’arco di meridiano che congiunge A con B come in figura 14 (traiettoria sinergica).
6. UNIVERSI PARALLELI ED UNIVERSI INTERSECANTI
Nel paragrafo precedente abbiamo considerato il caso di universi paralleli che, come tali, risultano incomunicanti.
Possiamo considerare ora il caso di universi che si intersecano, limitandoci necessariamente alle prime due dimensioni traendo delle conclusioni applicabili, per induzione, a spazi di ordine superiore.
In figura 15 possiamo osservare che l’intersezione di due spazi equipotenti, monodimensionali, dà luogo ad una intersezione zerodimensionale ed è necessario disporre di uno spazio bidimensionale per effettuare l’intersezione.
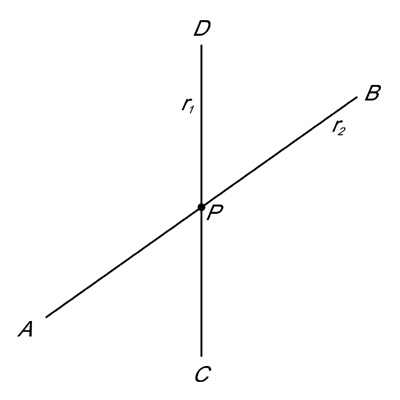
Figura 15 – Intersezione di due spazi monodimensionali
In figura 16 l’intersezione analoga a livello bidimensionale individua uno spazio monodimensionale ed è necessario disporre di uno spazio tridimensionale per effettuare l’intersezione.
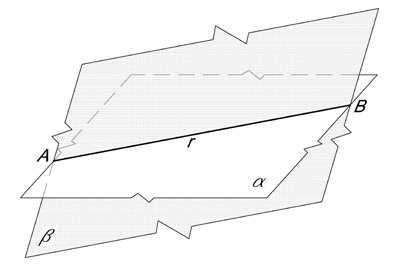
Figura 16 – Prospettiva dell’intersezione di due spazi bidimensionali
Non ci è possibile immaginare l’intersezione tra due spazi tridimensionali perché avremmo bisogno di lavorare su di uno spazio almeno quadrimensionale.
Queste osservazioni ci consentono di enunciare due Teoremi:
1) L’intersezione di due spazi di ordine n dà luogo ad un spazio di ordine n-1(n≠0);
2) Per intersecare due spazi di ordine n è necessario disporre di uno spazio di ordine ≥ n+1(n≠0).
Nel caso di spazi di ordine n≠0 e diverso tra loro possiamo immaginare soltanto un caso: l’intersezione tra un mono- ed un bi-dimensionale (monodimensionale∩bidimensionale in figura 17).
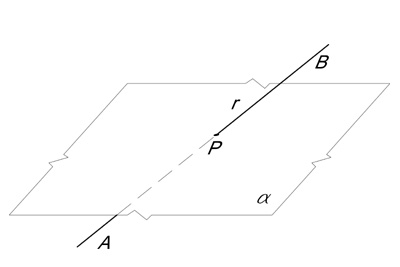
Figura 17 – Intersezione (α∩r) di due spazi di diverso ordine (mono- e bidimensionali)
Lo spazio bidimensionale α interseca lo spazio monodimensionale r definendo in tal modo uno spazio zerodimensionale P. E’ stato possibile realizzare l’operazione utilizzando una terza dimensione (di cui la figura 17 è, al solito, una prospettiva).
Ci sembra ragionevole generalizzare enunciando questi altri due Teoremi:
3) L’intersezione di due spazi di ordine m ed n (con m<n, m≠0 ed n≠0) dà luogo ad uno
spazio di ordine m-1;
4) Per intersecare due spazi di ordine m ed n (con m<n, m≠0 ed n≠0) è necessario operare
in uno spazio a n+1 dimensioni.
Oltre alle quattro citate proprietà è essenziale osservare una peculiare caratteristica posseduta dallo spazio tridimensionale:
esso è lo spazio con il minimo numero di dimensioni a possedere un volume diverso da zero; tale caratteristica dimensionale è essenziale affinché si possa realizzare un ciclo termodinamico (ovvero una sequenza di trasformazioni operate su di una massa che entri in un apparato con una certa quantità di energia e da questo esca tramite uno scarico dopo avere sviluppato e ceduto almeno parte di tale energia, in diversa forma, ad un sistema utilizzatore).
Per rendercene conto osserviamo la figura 18 che rappresenta un motore endotermico bidimensionale: per realizzare un ciclo è necessario un condotto d’aspirazione ed uno di scarico ma, senza un collegamento tubolare tra la parte alta (a tratto più marcato) e quella bassa (più in sottile) che necessariamente deve utilizzare almeno una terza dimensione, le due parti non “stanno insieme”.
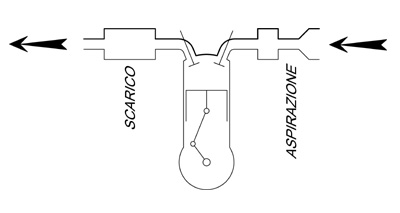
Figura 18 – Senza strutture tubolari (e quindi tridimensionali) non è possibile alcun ciclo termodinamico
Lo stesso dicasi per la vita animale (ed anche vegetale): senza strutture tubolari (si pensi al tubo digerente, come osserva Mikio Kaku, che è funzionale al motore endotermico costituito dall’apparato digerente degli animali) non sono possibili cicli termodinamici.
7. CONCLUSIONE
Acquisita la nozione di superspazio, o iperspazio che dir si voglia, proponiamo qualche riflessione applicativa.
In questo ambito la prima domanda potrebbe essere: quante dimensioni esistono?
Ci sembra ragionevole pensare che l’apparente tridimensionalità dell’universo sia dovuta alle limitate capacità sensoriali dell’uomo. Molti fatti storici e contemporanei inducono a pensare che esseri tridimensionali abbiano fruito, e fruiscano tuttora, di poteri attribuibili ad una loro capacità di percezione almeno quadrimensionale (apparizioni e sparizioni..., rubando la battuta ad Ezio Greggio!).
In base al Teorema 1) è necessario intersecare due spazi di ordine quattro per ottenere uno spazio di ordine tre il che significa postulare l’esistenza di almeno otto dimensioni; questa condizione soddisfa anche gli altri tre teoremi più sopra enunciati.
In omaggio al contra factum non valet argumentum cerchiamo di inquadrare i fatti storici e contemporanei, relativi alla vita umana, che trovano una comprensione ragionevole applicando le proprietà del superspazio:
Fase Uno: Il bimbo dal concepimento alla nascita potrebbe immaginare una vita perennemente vissuta nell’acqua,
suppergiù come un pesce sui generis, ma ciò che lo attende non è questo;
Fase Due: Il bimbo nasce, invecchia e muore avendo trovato condizioni di vita inimmaginabili in fase uno;
Fase Tre: Post mortem (ricordiamo i lavori di Raymond Moody sui casi di pre-morte e contra factum... checché ne
dicano gli scettici che, in omaggio al Pensiero Unico, antepongono l’ideologia alla Scienza) la parte
immortale dell’uomo acquisisce le sensibilità spaziali del superspazio. Ci sembra ragionevole pensare
che l’ente immortale, associato ad ogni uomo (che dovrebbe coincidere con l’anima nei pensieri di Platone e
di tanti Filosofi nonché di tanti Teologi, questi ultimi quando ci credono...), sia almeno tridimensionale ma in
grado di percepire forse tutte le almeno otto dimensioni fin qui postulate.
Anche questa condizione è inimmaginabile con certezza in fase due, mentre si possono distinguere nettamente
gli elementi di separazione tra le tre fasi (ciascuna delle quali assimilabile ad una funzione continua (1)):
concepimento, nascita, morte.
Le considerazioni fin qui sviluppate mancano del requisito della dimostrazione sperimentale che, almeno per ora, ci sembra impossibile: cataloghiamole nel ragionevole, non nello scientifico, visto che hanno una certa coerenza con fatti realmente avvenuti (e che tuttora avvengono) però non riproducibili in laboratorio.
Tra le tante applicazioni storiche delle proprietà del superspazio ci sia consentito, e ci appare molto interessante (ecco la ragione del sottotitolo!), pensare che la Natura abbia operato con tali proprietà (il nostro corpo tridimensionale è "aperto" alle azioni di un altro essere, pur tridimensionale, ma in grado di percepire almeno la quarta dimensione) quando ha visto la luce il Bambinello, donatoci dall’Immortale Fanciulla di Nazareth, senza violarne la Verginità.
(1) Appendice: L’Equazione del Bambino (The Kid Equation)
Quando il bambino si trova nella Fase Uno è soggetto ad una evoluzione la cui continuità può essere espressa come segue:
Indichiamo con Ψ il suo stato, stato che cambia in funzione del tempo t (quindi possiamo scrivere Ψ = Ψ(t)): il lettore può pensare che ad ogni stato corrisponda una fotografia istantanea.
L’intervallo di definizione di tale stato sia il periodo t di gestazione
0 ≤ t ≤ 9 mesi.
Indicato con ε un intervallo di tempo positivo, piccolo a piacere, una nuova istantanea rappresenterà lo stato Ψ(t+ε).
Per tutto l’intervallo di definizione vale la seguente uguaglianza:
.jpg)
ovvero non esiste alcun momento singolare che differenzi in modo qualitativo lo stato del bambino nell’intervallo di tempo della gestazione (Equazione del Bambino).
Poniamo che, nell’intervallo di tempo considerato, il bambino abbia un “incidente” per cui sia costretto (più o meno violentemente) a saltare la Fase Due passando direttamente alla Fase Tre: sarà possibile, allora, determinare una discontinuità netta tra due stati successivi, in tale intervallo, in modo che si verrà a verificare la seguente, infausta, disuguaglianza:
.jpg)
In questo caso il nostro little boy non c’e l’ha fatta...
L'artiglio rapace dell'Erode di turno ha provocato un cambiamento di stato repentino ed innaturale (dal ventre della mamma al secchio).
Nel link indicato la nascita di Gesù vista da Maria Valtorta. Opera dell'amico Max...
piermariaboria@alice.it - La conservata verginità di Maria si può spiegare (ci sembra una spiegazione convincente) con le proprietà di una quarta dimensione.
www.piermariaboria.it
 Link a file di approfondimento
Link a file di approfondimento